Summary
This is a lesson for Law of Cosines, which also connects Law of Sines and Law of Cosines to map triangulation. Students will receive a brief introduction to Trig Pillars: a tool used in the United Kingdom in the mid-20th century to help with mapmaking. Then, they will go through an informal proof of the Law of Cosines. Students will apply what they have learned to calculate distances across a school map. Law of Sines is a prerequisite for this lesson.
Essential Question(s)
How can indirect measurements help calculate unknown distances?
Snapshots
Engage
Students watch a quick video about Trig Pillars in the United Kingdom.
Explore
Students work through an informal proof of Law of Cosines.
Explain
Students generalize the Law of Cosines and formalize their understanding through class discussion.
Extend
Students practice map triangulation on a school map.
Evaluate
Students reflect on their learning and compare Law of Sines and Law of Cosines.
Materials
Lesson Slides (attached)
Proof Process handout (attached; one per student; printed front/back)
School Map handout (attached; one per student; printed front only)
Calculating Distance handout (attached; one per student; printed front only)
Calculating Distance (Sample Responses) document (attached; for teacher use)
Protractors
Straightedges
Scientific calculators
Engage
10 Minute(s)
Introduce the lesson using the attached Lesson Slides. Slide 3 displays the lesson’s essential question. Slide 4 identifies the lesson’s learning objectives. Review each of these with your class to the extent you feel necessary.
Display slide 5 and show students The Concrete Pillars On Top Of British Hills: Trig Points video, which gives students a brief overview of Triangulation Pillars, also known as Trig Points/Pillars, that are throughout the United Kingdom. These pillars were constructed and used during the mid-20th century by the Ordinance Survey to retriangulate the United Kingdom.
Show slides 6–7, which provide a bit more background information about Trig Pillars and the purpose of triangulation in calculating distances. Tell students that today they will learn how to use trigonometry to determine unknown distances.
Explore
15 Minute(s)
Display slide 8 and pass out the Proof Process handout to each student. Allow them some time to work through the steps on their own. After about 7 minutes of working on their own, show slide 9 and have them share their answers with a partner and compare their progress using the Inverted Pyramid strategy. If their answers are not the same, give them a few minutes to talk through the differences and decide which answers they can agree to.
Explain
15 Minute(s)
Once students compare with a partner, continue the Inverted Pyramid by having a whole-group discussion.
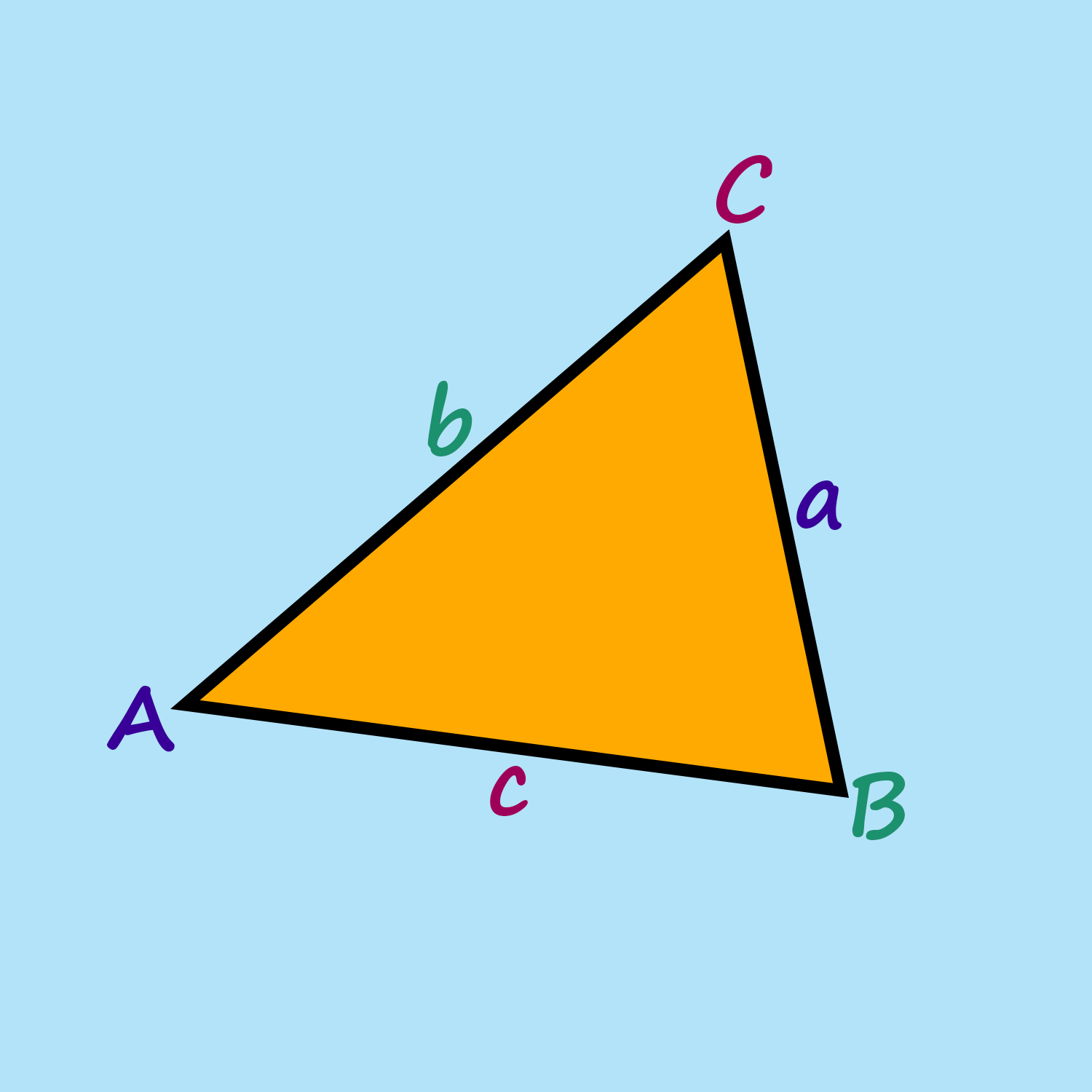
Show slide 12, displaying the Law of Cosines, the result to the Proof Process handout: c2 = a2 + b2 – 2ab·cos(C). Tell students that this should be their final result. Ask them, "How did you do?" After a few answers, ask, "If you got it wrong, where did you go wrong?" Once again, allow students time to discuss, share, and fix their work.
Then, direct students to look at both the correct equation and the triangle diagram from the Explore activity. Ask students what specific components are needed to make Law of Cosines valid or usable.
Finally, based on their ideas, prompt students to write equations solved for the other side lengths, a and b. Give students about 3 minutes to write out the equations, and then show them the correct answers on slide 13. Give them a moment to correct as needed. Before moving on, make sure that students have made the connection between the adjacent sides and the contained angle being the needed information to use the Law of Cosines.
Extend
35 Minute(s)
Show slide 14 and pass out a School Map handout and a Calculating Distance handout to each student.
Since students use each answer in their following calculations, show slides 15–16 to make sure that students understand steps 1–2 of the activity and start the activity correctly. Then have students work independently to complete the activity. It is a productive challenge for them to try the activity independently, but if they struggle to do the activity on their own, have them work in pairs. If students follow the prompts correctly, then they will construct triangles on the school map, using a straightedge and protractor, and will utilize Law of Sines or Law of Cosines to calculate unknown distances on the school map. Use the hidden slide 17 for quick reference regarding students’ accuracy as you monitor the activity. Remember that there will be variety in your students’ results. See the Calculating Distance (Samples Responses) document for more guidance.
Evaluate
5 Minute(s)
Show slide 18 and instruct students to turn over their Calculating Distance handout to answer the questions on the slide on the back of their handout.
In which situation(s) did you use the Law of Sines?
In which situation(s) did you use the Law of Cosines?
In which situation(s) could you have used the Law of Cosines? In which situation(s) could you have not? Justify your answers.
What information could be used to determine if the Law of Sines or Law of Cosines is the most appropriate for the situation?
Collect the Calculating Distance handout to assess student learning. Look at their responses to check that students understand that to find the length of the side of a triangle, they need two angles and one opposite side to use the Law of Sines, and they need two sides and the included angle to use the Law of Cosines.
If time allows, have a class conversation about this distinction. In general, the Law of Cosines is best for finding the length of the third side of a triangle when the other two side lengths and included angle are known. The Law of Sines is best used to find the length of the third side of a triangle when two angles and one side length is given or to find the third side length when two sides and the non-included angle are known. Both formulas can be used to find unknown angles as well. Students at this point should start to be able to make the decision of which formula is most appropriate for a given situation. If students struggle with identifying the right formula to use, consider giving students a series of problems where the task is not to perform the calculations to find the missing information but to simply identify the right tool to complete the task. When doing this, be sure to have students justify why they picked Law of Sines or Cosines; this will help reinforce when to use each formula.
Resources
Johnson, H. L. (n.d.). Law of Cosines: Lesson 2. NCTM. https://illuminations.nctm.org/lesson.aspx?id=2441
K20 Center. (n.d.). Inverted Pyramid. Strategies. https://learn.k20center.ou.edu/strategy/173
K20 Center. (n.d.). Law of Sines. 5E Lessons. https://learn.k20center.ou.edu/lesson/2549
Newman, J. (2013). Law of Sines/Cosines "Mapquest" [Blog post]. Hilbert’s Hotel. https://hilbertshotel.wordpress.com/2013/01/10/law-of-sinescosines-mapquest/
Scott, T. (2014, December 8). The concrete pillars on top of British hills: Trig points [Video]. YouTube. https://www.youtube.com/watch?v=VxBlyZAl5MQ
Staziker, T. (2016, February 19). Mountain Trig Point Summit [Photograph]. Pixabay. https://pixabay.com/photos/mountain-trig-point-summit-1519813/