Summary
In this lesson, students will recall finding greatest common factors (GCFs) of polynomials and the relationship between the factored and standard forms of a quadratic expression. Then, students will learn how to factor using the TRI method. Students will use this knowledge to factor and solve (factorable) quadratics with any leading coefficient.
Essential Question(s)
How can we solve quadratic equations by factoring?
Snapshot
Engage
Students recall finding greatest common factors through a card game.
Explore
Students match factors or GCFs with quadratic expressions to solve a hexagon puzzle.
Explain 1
Students watch a video and complete guided notes with the class and formalize their understanding of the TRI method of factoring where the leading coefficient is 1.
Extend 1
Students apply what they have learned to factor quadratic expressions and solve quadratic equations with a leading coefficient of 1.
Explain 2
Students watch a video and complete guided notes with the class. Students solidify their understanding of the TRI method of factoring by working with quadratics with a leading coefficient other than one.
Extend 2
Students apply what they have learned to factor quadratic expressions and solve quadratic equations with a leading coefficient other than 1.
Evaluate
Students reflect on their learning and demonstrate their understanding of the TRI method of factoring using the Why-Lighting strategy.
Materials
Lesson Slides (attached)
GCF Card Game document (attached; one set per group; printed front only)
Hexagon Puzzle handout (attached; one per pair; printed front only)
Guided Notes handout (attached; one per student; printed front and back)
Guided Notes (Model Notes) document (attached)
TRI Factoring handout (attached; one per pair; printed front only)
TRI Factoring Again handout (attached; one per pair; printed front only)
Why-Lighting Factors handout (attached; one per student; printed front only)
Pencils
Highlighters
Paper
Scissors
Glue sticks (optional; one per pair)
Engage
15 Minute(s)
Introduce the lesson using the attached Lesson Slides. Display and review the essential question on slide 3. Move to slide 4 and review the lesson’s learning objectives.
Instruct students to get into groups of 2–3 or assign groups. Display slide 5 and pass out the prepared TRI Game cards. Explain the rules and objective of the game.
Have students play in small groups. They should place nine cards face up on their table so that everyone in their group can see and reach them. Then, students should look for sets of three cards that have a greatest common factor containing a letter and a coefficient greater than one (these are known as TRI sets). In other words, the GCF could be 2x2 or 2x, but could not just be 2 or just x.
Use the example and non-example on the slide to clarify the rules. In their small groups, the first student to see a TRI set says "TRI" (from the prefix meaning three) and the game pauses. That player points to the three cards and shares the GCF with the group. The other player(s) check the GCF, if that player is correct, then they collect the 3 cards. If that player is incorrect, then the person who corrected the player collects the three cards into their winning pile.
The goal is to have the most cards at the end of the game, and the game ends when there are no more TRI sets or cards to draw. The game could also be ended early with a timer. Timers can be found on the K20 Center’s YouTube channel.
Explore
20 Minute(s)
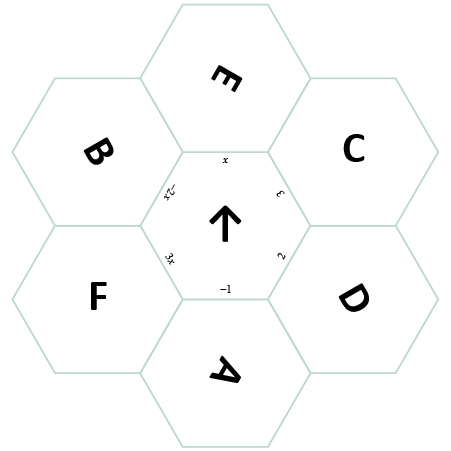
Move to slide 6 and have students get into pairs. Pass out scissors and the attached Hexagon Puzzle handout to each pair. Ask students to cut out the seven hexagons and rearrange them into a flower pattern like the one shown on the slide, such that the sides touching are equivalent expressions or are an expression and its GCF.
As students work together to solve the puzzle, use the image below as a quick way to check students’ work. This image is also available on the hidden slide 7. Once the arrow on the center hexagon is pointing up, the letters should be oriented as shown.
Explain 1
10 Minute(s)
Pass out the attached Guided Notes handout to each student and display slide 8. Play the "TRI Factoring, Part A" video for the students and ask them to complete only the front of the Guided Notes as they watch the video. Use the attached Guided Notes (Model Notes) document to see what the notes should look like.
Once students have completed only the front side of the notes, ask them to set it aside. The other side will be completed later in the lesson.
Extend 1
20 Minute(s)
Display slide 9 and give each student a copy of the attached TRI Factoring handout Then, direct their attention to the first part of the handout: Factoring Quadratics. Have students work with a partner of their choice or assign partners to complete this handout. Ask students to factor each expression from questions 1-4 with their partner.
As you see students finishing question 2, display slide 10. Bring the class together for questions and discussion. Ask for volunteers to explain how they factored questions 1–2. This slide shows the questions, the answers, and part of the TRI method: the GCF, the factors of a, and the factors of c.
When this discussion has concluded, ask students to complete questions 3-4 and discuss how they are both similar and different.
Then, as students finish question 4, move to slide 11. Bring the class together for questions and discussion. Ask for volunteers to explain how they factored questions 3–4. This slide shows the questions and answers. If time allows, consider asking student to go to the board to show their work.
Display slide 12 and direct students’ attention to the second part of their handout: Solving Quadratics. Review the process of solving quadratics using factoring with the class. Then ask the class the question from the slide: Why must one side of the equation equal zero before you start factoring?
Give all students a chance to consider this question. Then, have students discuss their answer with their partner. After a couple of minutes of discussion, ask for volunteers to explain their thinking.
Move to slide 13 and have students continue to work in pairs to solve the quadratic equations by factoring to finish the handout.
As students progress through questions 5–8, transition through slides 14–16 so students can check their work.
Explain 2
10 Minute(s)
Have students return to their Guided Notes handout and display slide 17. Play the "TRI Factoring, Part B" video and direct students to complete the back of the Guided Notes as they watch the video.
After completing the handout, direct students to add this to their math notebook if that is a classroom norm.
Extend 2
25 Minute(s)
Now it is time for students to apply what they have learned. Display slide 18 and give each student a copy of the attached TRI Factoring Again handout. Direct their attention to the first part of the handout: Factoring Quadratics. Instruct students to factor each expression on questions 1–4 with their partner and discuss the similarities and differences between questions 2 and 4.
As you see students finishing question 4, display slide 19 and bring the class together for questions and discussion. Ask for volunteers to explain how they factored questions 1–4.
Now direct students’ attention to the second part of their handout: Solving Quadratics. Challenge students to now work independently to solve the quadratic equations on questions 5–8.
As students progress through questions 5–8, transition through slides 20–22 so students can check their work.
Evaluate
10 Minute(s)
Move to slide 23 and introduce students to the Why-Lighting strategy. Pass out the attached Why-Lighting Factors handout to each student. Instruct them to highlight the critical details that help them make decisions when factoring and to write why they highlighted them in the margins of the handout.
Once students are finished, ask them to find a new partner (someone who they have not yet worked with during this lesson) to share their reasoning for what they highlighted. Working with different peers encourages the development of academic vocabulary and encourages students to consider different approaches to a problem.
After students have had a few minutes to share with their partner, bring the class together for questions and discussion. Ask for volunteers to share what they highlighted and their reasoning, then facilitate a discussion asking the class to compare the similarities and differences between the columns on the handout.
Once students understand quadratics and are ready to learn how to factor other polynomials, use the "Finding Factors, Part 2" lesson. It focuses on a difference of squares, sums and differences of cubes, and grouping.
Resources
K20 Center. (n.d.). Why-Lighting. Strategies. https://learn.k20center.ou.edu/strategy/128
K20 Center. TRI Factoring, Part A. YouTube. https://youtu.be/2FGYijGLa2c
K20 Center. TRI Factoring, Part B. YouTube. https://youtu.be/DGc0VQiDsz4



