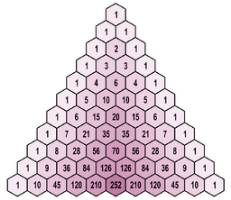
Summary
In this lesson, students will have opportunities to explore patterns found in Pascal's triangle with the intent of using these patterns to expand binomial expressions. This lesson is Part 1 of 2. The goal of this lesson is to look at connections between binomial expansion and Pascal's triangle. Part 2 connects this lesson to the binomial theorem.
Essential Question(s)
What patterns emerge in Pascal's triangle, and how can they connect to binomial expression expansion?
Snapshot
Engage: Students investigate the patterns that form Pascal's triangle.
Explore: Students work together to expand binomials using traditional methods and compare their results to what they see in Pascal's triangle.
Explain: Students work in groups to articulate the patterns they see and share with their classmates.
Extend: Students work in groups on more complicated binomial expansion using their newly constructed knowledge of Pascal's triangle.
Evaluate: Students self-assess their work and complete an Exit Ticket.
Materials
Binomial Expansion Exploration handout (attached; one per student)
Blank Pascal's Triangle handout (attached; one per student)
Window Notes for Math handouts (attached; one per student)
Pens or pencils
Scratch paper
Engage
Introduce the lesson using the attached Lesson Slides. Slide 3 displays the lesson’s Essential Question: What patterns emerge in Pascal’s triangle, and how can they connect to binomial expression expansion? Slide 4 identifies the lesson’s learning objectives. Review each of these with your class to the extent you feel necessary.
Display slide 5. To begin, distribute the attached Blank Pascal's Triangle handout to each student.
With students, construct the first three or four rows of Pascal's triangle. DO NOT TELL STUDENTS THE PATTERN OR HOW TO FIND THE PATTERN. This is something they will discover as they continue to engage in the activity.
Ask students to work in pairs to see if they can determine the patterns needed to fill in the missing numbers for the remaining triangle.
Once students determine the pattern of Pascal's triangle, ask them to share with another pair of students.
As a whole class, invite students to share what they believe the pattern to be.
Explore
Distribute copies of the attached Binomial Expansion Exploration handout.
Go to slide 6. Ask students to work in pairs or in their groups of four to expand the binomials on part one (1) of the handout.
Be sure to move around the room to help students clarify their work, asking probing questions to help them arrive at the correct binomial expansions.
When students finish part 1, have them move on to part 2 of the handout. Part 2 asks students to make connections between coefficients in their expanded binomials and what they see in Pascal's triangle.
Explain
Go to slide 7. In order to clarify misconceptions about the topic, ask students to complete part 3 of the Binomial Expansion Exploration handout.
For part 3, students will follow the instructions in the handout to do the following:
Find a partner in a different group.
Compare and contrast their answers to parts 1 and 2 of the handout.
Return to their original groups to share new insights they might have learned.
Extend
Display slide 8. Ask students to work in their small groups to complete part 4 of the handout. This activity is intended to move students past the generic binomial form to more complex problems.
As students work through part 4, ask them to fill in the Window Notes handout squares.
Evaluate
Display slide 9. In small groups, ask students to share the questions they have from the Binomial Expansion and Window Notes handouts.
As questions come up, ask students to help their peers who have questions come to an understanding of the problems at hand.
Ask students to take out a blank sheet of paper. As students leave for the day, ask them to reflect on their learning using the What? So What? Now What? strategy.
What? Literally, what did you do?
So what? Why does it matter?
Now what? What will you take with you? How do you think this might connect to other areas of mathematics?
Resources
K20 Center. (n.d.). What? So what? Now what?. Strategies. https://learn.k20center.ou.edu/strategy/b30762a7557ba0b391f207f4c6002113
K20 Center. (n.d.). Window notes. Strategies. https://learn.k20center.ou.edu/strategy/fc74060730ea745c8c4f356aa2015ac0
Khan Academy. (n.d.) Pascal's triangle and binomial expansion. [Video]. https://www.khanacademy.org/math/precalculus/x9e81a4f98389efdf:polynomials/x9e81a4f98389efdf:binomial/v/pascals-triangle-binomial-theorem
The Organic Chemistry Tutor. (2016, December 4). Binomial Theorem Expansion, Pascal's Triangle, Finding Terms & Coefficients, Combinations, Algebra 2. YouTube. https://www.youtube.com/watch?v=s19dWIHficY